Estudo da Reta
Equação geral da reta: toda reta r do plano cartesiano pode ser representada por uma equação:
ax + by + c = 0
Onde
x e y são coordenadas de um ponto genérico pertencente a r e a, b e c
são números reais, sendo a e b não nulos ao mesmo tempo.
1) Determine a equação geral da reta que passa pelos pontos: A(–1, 2) e B(–2, 5).
[– 5 + 2x + (–2y)] – [(– 4) + (– y) + 5x] = 0
[– 5 + 2x – 2y] – [– 4 – y + 5x] = 0
– 5 + 2x – 2y + 4 + y – 5x = 0
–3x – y – 1 = 0
A equação geral da reta que passa pelos pontos A(–1, 2) e B(–2, 5) é dada pela expressão: –3x – y – 1 = 0.
Equação segmentária da reta: a equação de uma reta r que intercepta os eixos nos pontos distintos da origem N (0, n) e P (p, 0), pode ser obtida da seguinte forma:
[– 5 + 2x + (–2y)] – [(– 4) + (– y) + 5x] = 0
[– 5 + 2x – 2y] – [– 4 – y + 5x] = 0
– 5 + 2x – 2y + 4 + y – 5x = 0
–3x – y – 1 = 0
A equação geral da reta que passa pelos pontos A(–1, 2) e B(–2, 5) é dada pela expressão: –3x – y – 1 = 0.
Equação segmentária da reta: a equação de uma reta r que intercepta os eixos nos pontos distintos da origem N (0, n) e P (p, 0), pode ser obtida da seguinte forma:
Sendo:
1) Determine a forma segmentária da equação da reta s cuja equação geral é:
s: 2x + 3y – 6 = 0
s: 2x + 3y – 6 = 0
Determine a área do triângulo de vértices A (1, 3), B (2, 5) e C (-2,4).
Solução: Primeiro devemos realizar o cálculo do determinante.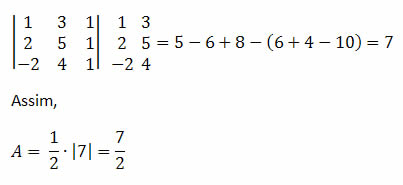
Solução: Primeiro devemos realizar o cálculo do determinante.
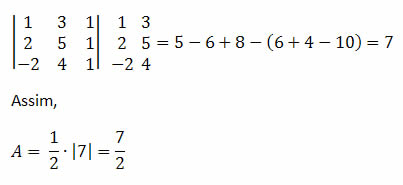
Para determinar a equação segmentária da reta s devemos isolar o termo independente c. Assim, segue que:
2x + 3y = 6
Dividindo a equação por 6, obtemos:
A identidade acima é a forma segmentária da equação da reta s.
2x + 3y = 6
Dividindo a equação por 6, obtemos:

A identidade acima é a forma segmentária da equação da reta s.
Coeficiente angular de uma reta: num sistema cartesiano ortogonal, a reta r, não vertical, forma com Ox um ângulo com medida alfa. Essa reta r tem como coeficiente angular um número real m dado por tg de alfa. Observe:
- Quando o ângulo é nulo, então m é zero.
- Quando o ângulo é agudo, então m é positivo.
- Quando o ângulo é obtuso, então m é negativo.
No triângulo formado por A, B e C, a tg alfa é determinada por:
Equação reduzida da reta: pode-se determinar a equação reduzida de r, isolando o valor de y em função de x.
Sendo:
- coeficiente angular (m) da reta;
- coeficiente linear (n) da reta:
1) A equação reduzida de uma reta de acordo
com os pontos P(2, 7) e Q(–1, –5) pertencentes à reta. Para determinar
essa equação há duas maneiras, observe:
1º maneira
Determinar o coeficiente angular da reta.
m = (y2 – y1) / (x2 – x1)
m = (–5 – 7) / (–1 – 2)
m = –12 / –3
m = 4
m = (–5 – 7) / (–1 – 2)
m = –12 / –3
m = 4
De acordo com o ponto P(2, 7), temos:
y – y1 = m * (x – x1)
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8
y = 4x – 8 + 7
y = 4x – 1
y – 7 = 4 * (x – 2)
y – 7 = 4x – 8
y = 4x – 8 + 7
y = 4x – 1
2ª maneira
Temos que a lei de formação de uma equação reduzida da reta é dada por y = mx + c.
Considerando que ela passa por P(2, 7) e Q(–1, –5), temos:
P(2, 7)
7 = m * 2 + c
7 = 2m + c 2m + c = 7
7 = 2m + c 2m + c = 7
Q(–1, –5)
–5 = m * (–1) + c
–5 = –m + c –m + c = –5
–5 = –m + c –m + c = –5
Nesse caso, os valores dos coeficientes angular (m) e linear (c) serão calculados por um sistema de equações. Veja:
Isolando c na 2ª equação:
–m + c = –5
c = –5 + m
c = –5 + m
Substituindo c na 1ª equação:
2m + c = 7
2m + (–5 + m) = 7
2m – 5 + m = 7
3m = 7 + 5
3m = 12
m = 12/3
m = 4
2m + (–5 + m) = 7
2m – 5 + m = 7
3m = 7 + 5
3m = 12
m = 12/3
m = 4
Calculando o valor de c:
c = –5 + m
c = –5 + 4
c = –1
c = –5 + 4
c = –1
Portanto, a equação reduzida da reta que passa pelos pontos P(2, 7) e Q(–1, –5), corresponde à expressão y = 4x – 1.
Equação da reta, conhecidos um ponto e a direção
- Pode-se determinar, quando a reta não é vertical, pela fórmula:
- Quando a reta for vertical, determina-se pela fórmula:
x = xa
Equações paramétricas da reta: são equações paramétricas de uma reta s onde f (t) e g (t) expressam leis de funções do primeiro grau.
x = f (t)
y = g (t)
Posição relativa de duas retas no plano cartesiano
- r e s são paralelas, quando:
- r e s são coincidentes, quando:
- r e s são concorrentes, quando:
- r e s são perpendiculares, quando:
Ângulos entre duas retas
Considerando r e s, retas não verticais, concorrentes mas não perpendiculares entre si:
A medida do ângulo agudo:
A medida do ângulo obtuso:
OBS: Caso r seja vertical, então:

Distância entre ponto e reta: a distância entre o ponto P (xp, yp) e a reta (r) ax by + c = 0, pode ser calculada utilizando a fórmula:
1) O ponto A(–1, –2) é um vértice de um triângulo equilátero ABC, cujo lado
BC está sobre a reta de equação x + 2y – 5 = 0. Determine a medida h da
altura desse triângulo.
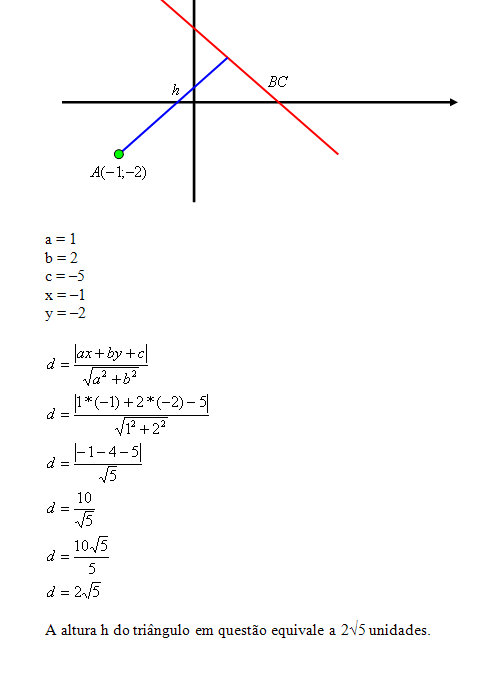
Área de um triângulo ABC: cujos vértices são os pontos A (xa, ya), B (xb, yb) e C (xc, yc), pode ser calculada da seguinte forma:
1) Calcule a área do triângulo de vértices A (4 , 0), B (0 , 0) e C (0 , 6).
Primeiro passo é fazer o cálculo do determinante das coordenadas dos pontos A, B e C. Teremos:

Assim obtemos:
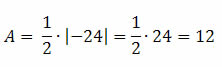
Portanto, a área do triângulo de vértices A (4 , 0), B (0 , 0) e C (0 , 6) é 12.
2) Os pontos A (0, 0), B (0, -8) e C (x, 0) determinam um triângulo de área igual a 20. Encontre o valor de x.
Sabemos que a área do triângulo de vértices A, B e C é 20. Então,

Estudo Analítico da Circunferência
Equação reduzida da circunferência: considerando uma circunferência, de raio r e centro C (xc, yc) num plano alfa, pode-se obter a equação reduzida pela fórmula:
Equação geral da circunferência: a partir da equação reduzida de uma circunferência, de raio r e centro C (xc, yc) é que pode-se chegar a equação geral:
- O termo independente é:

- O raio é:
- A equação geral da circunferência é do 2º grau em x e em y.
- Os coeficientes de x² e y² são iguais e diferentes de zero.
- Não apresenta o termo x y, isto é, pode-se considerar que o seu coeficiente é zero.
Posições do ponto P em relação à circunferência
Onde:
n = x²p + y²p - 2xcxp - 2ycyp + (x²c + y²c - r²)
Posições da reta s em relação à circunferência
Posições relativas de duas circunferências
quando:
- externamente:
1) O ponto P(3, b) pertence à circunferência de centro no ponto C(0, 3) e raio 5. Calcule valor da coordenada b.
Temos por (x – a)² + (y – b)² = r², que a circunferência de centro C(0 ,3) e raio 5, possui como representação a equação (x – 0)² + (y – 3)² = 5² ou x² + (y – 3)² = 25.
Considerando que o ponto P(3, b) pertença à circunferência, então:
x² + (y – 3)² = 25
3² + (b – 3)² = 25
9 + (b – 3)² = 25
(b – 3)² = 25 – 9
(b – 3)² = 16
b – 3 = 4 ou b – 3 = – 4
b = 4 + 3 ou b = –4 + 3
b = 7 ou b = –1
A coordenada b pode assumir os valores 7 ou –1.
2) Determine a equação da circunferência que possui centro em C(3, 6) e raio 4.
A equação da circunferência de centro C(a, b) e raio r, com r > 0, é (x – a)² + (y – b)² = r².
Portanto:
A equação da circunferência com coordenados do centro (3, 6) e raio medindo 4 é dada por:
(x – 3)² + (x – 6)² = 16
3) Dada as equações das circunferências λ1 : x² + y² – 4x – 8y – 5 = 0 e λ2 : x² + y² – 2x – 6y + 1 = 0, determine se elas possuem pontos em comum.
Resolvendo o sistema 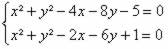 , determinaremos se possuem pontos em comum.
, determinaremos se possuem pontos em comum.

Resolvendo o sistema por Adição:
– 2x – 2y – 6 = 0 → – x – y – 3 = 0 → –y = x + 3 → y = – 3 – x
Substituindo y em qualquer das equações:
x² + y² – 4x – 8y – 5 = 0
x² + (–3–x)² – 4x – 8y – 5 = 0
x² + x² + 6x + 9 – 4x + 8x + 24 – 5 = 0
2x² + 10x + 28 = 0
Resolvendo a equação por Bháskara:
? = b² – 4ac
? = 10² – 4 * 2 * 28
? = 100 – 224
? = – 124
Em razão de delta menor que 0, a equação não possui raízes reais. Logo, as circunferências não possuem pontos em comum.
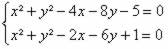 , determinaremos se possuem pontos em comum.
, determinaremos se possuem pontos em comum.

Resolvendo o sistema por Adição:
– 2x – 2y – 6 = 0 → – x – y – 3 = 0 → –y = x + 3 → y = – 3 – x
Substituindo y em qualquer das equações:
x² + y² – 4x – 8y – 5 = 0
x² + (–3–x)² – 4x – 8y – 5 = 0
x² + x² + 6x + 9 – 4x + 8x + 24 – 5 = 0
2x² + 10x + 28 = 0
Resolvendo a equação por Bháskara:
? = b² – 4ac
? = 10² – 4 * 2 * 28
? = 100 – 224
? = – 124
Em razão de delta menor que 0, a equação não possui raízes reais. Logo, as circunferências não possuem pontos em comum.



























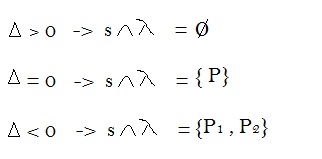










Nenhum comentário:
Postar um comentário